Oracle Spatial的GIS空间数据模型

      Oracle Spatial 是Oracle数据公司提供的一个扩展产品，它具有专门的空间数据管理功能。Oracle Spatial提供了三种最主要的几何类型（点、线、面世以及由这些几何类型对象组合而成的集合。这三种几何类型又可分为简单点（只有一个点）、点群（有多个点）、简单线（只有一条线）、线群（有多条线）、简单面（只有一个面）、面群（有多个面）。因此Oracle Spatial一共提供了七种几何类型，并为每种类型分配了从1~7的标识。同时，在有的类型中，还划分了更详细的类型，如简单线还可分为线段、三点圆弧、线段和圆弧交替连接的简单复合线等，简单面可分为由线段构成的面、圆、矩形、线段和圆弧交替连接的简单复合面。

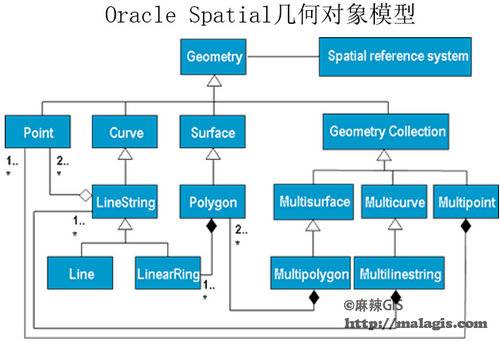
      1.几何对象（Geometry）

      是几何对象层次模型的根类,它是一个抽象类(不可实例化).在二维空间坐标中, Geometry的可实例化的子类被限制定义为零维、一维、二维几何对象。

      2.几何集合对象（Geometry Collection）

      Geometry Collection是一个或多个Geometry对象的集合。在这个集合中的所有元素都必须有同样的空间参考，这个空间参考也就是该Geometry Collection的空间参考。

     3.点（Point）

      Point是零维的几何对象，表示空间中一个单个的位置信息。

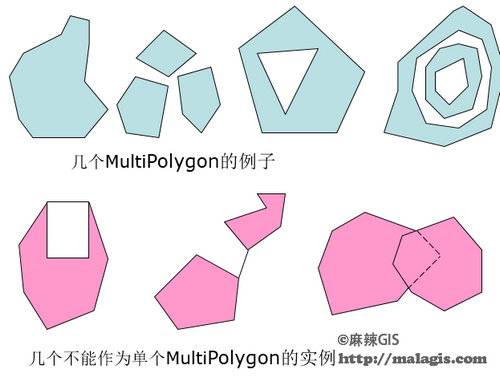
     4.多点（MultiPoint）

     MultiPoint是零维几何对象的集合， MultiPoint中的元素必须是Point，Point之间不是相连的或是有序的。若没有任何两个点是等同的，则MultiPoint是简单的。

     5.曲线（Curve）

     Curve是一维几何对象，通常作为一序列点来存储。

     6.折线（LineString），直线段（Line），线性环（LinearRing）

     OGC定义了一个Curve的子类LineString， LineString在两点之间采用了线性插值。 Line是只有两个点的LineString。LinearRing是一个闭合的“简单”的LineString

     7.多曲线（MultiCurve）

      MultiCurve是一个一维的几何对象集合，其元素都是Curve。

     8.多折线（MultiLineString）

     当MultiCurve的所有元素都是LineString时，它可被定义为Multi LineString。

     9.面（Surface）

     Surface是二维的几何对象。OGC的定义了一个“简单”的Surface：它是由一个单独的小片（Path）关联1个外圈，0个或多个内圈。在三维空间中“简单”的Surface等价于平面的Surface。二维空间的多面体是通过将Surface的边界“缝合”而成的。

     简单的Surface的边界是由相关于它的外圈和内圈的闭合的Curve组成。Surface唯一可实例化的子类是Ploygon，它是一个简单的、平面的Surface。

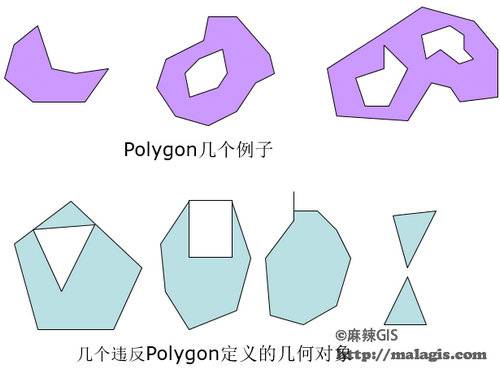
     10.多边形（Polygon）

     Polygon是平面的Surface，是由一个外圈和0个或多个内圈组成。每个内圈被认为是Polygon的一个“岛”。关于Polygon的一些定义。

     Polygon是拓扑闭合的

     Polygon的边界是由一组LineString（线环）组成，这些LineString形成它的外边界和内边界。

     在Polygon的边界中，任意两个LineString都不是相互穿越的。

     每个Polygon内部是连续的点集

     11.多面（MultiSurface）

     MultiSurface是二维的几何对象集合,它的元素都是Surface.在MultiSurface中,任意两个Surface的内部都不可以相交,任何两个元素的边界可以相交于有限的点.

     12多个多边形（MultiPolygon）

      当MultiSurface的所有元素都是Polygon时,它被定义为MultiPolygon.关于MultiPolygon的声明.