全国高分辨率土地利用数据服务 土地利用数据服务 土地覆盖数据服务 坡度数据服务 土壤侵蚀数据服务 全国各省市DEM数据服务 耕地资源空间分布数据服务 草地资源空间分布数据服务 林地资源空间分布数据服务 水域资源空间分布数据服务 建设用地空间分布数据服务 地形、地貌、土壤数据服务 分坡度耕地数据服务 全国大宗农作物种植范围空间分布数据服务
多种卫星遥感数据反演植被覆盖度数据服务 地表反照率数据服务 比辐射率数据服务 地表温度数据服务 地表蒸腾与蒸散数据服务 归一化植被指数数据服务 叶面积指数数据服务 净初级生产力数据服务 净生态系统生产力数据服务 生态系统总初级生产力数据服务 生态系统类型分布数据服务 土壤类型质地养分数据服务 生态系统空间分布数据服务 增强型植被指数数据服务
多年平均气温空间分布数据服务 多年平均降水量空间分布数据服务 湿润指数数据服务 大于0℃积温空间分布数据服务 光合有效辐射分量数据服务 显热/潜热信息数据服务 波文比信息数据服务 地表净辐射通量数据服务 光合有效辐射数据服务 温度带分区数据服务 山区小气候因子精细数据服务
全国夜间灯光指数数据服务 全国GDP公里格网数据服务 全国建筑物总面积公里格网数据服务 全国人口密度数据服务 全国县级医院分布数据服务 人口调查空间分布数据服务 收入统计空间分布数据服务 矿山面积统计及分布数据服务 载畜量及空间分布数据服务 农作物种植面积统计数据服务 农田分类面积统计数据服务 农作物长势遥感监测数据服务 医疗资源统计数据服务 教育资源统计数据服务 行政辖区信息数据服务
Landsat 8 高分二号 高分一号 SPOT-6卫星影像 法国Pleiades高分卫星 资源三号卫星 风云3号 中巴资源卫星 NOAA/AVHRR MODIS Landsat TM 环境小卫星 Landsat MSS 天绘一号卫星影像

一.地图投影(map projection)的基本概念
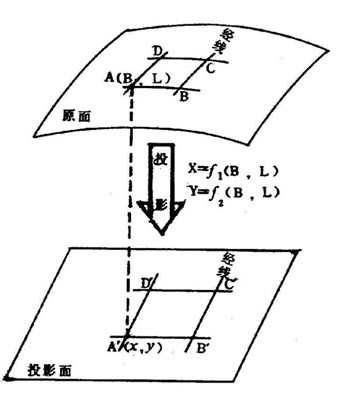
地图投影是将地球椭球面上的点投影到平面上的数学方法。其实质就是建立地球椭球面上点与平面上对应点之间的函数关系。
其数学公式为:X=f1(ϕ,λ)X=f1(ϕ,λ)Y=f2(ϕ,λ)Y=f2(ϕ,λ)当给定不同的具体条件时,就可以得到不同种类的投影。
下面是投影的简单示意图:
二.投影变形(Projection distortion)
长度变形(distance distortion)
即长度比与1之差值,vμ=μ−1vμ=μ−1所谓长度比(distance scale)是指:地面上微分线段投影后的长度ds’与其相应的实地长度ds之比,
μ=ds′/dsμ=ds′/ds极值长度比:一点上不同方向上的长度比是不同的,其中最大值和最小值,称为极值长度比,用a和b来表示。
主方向:极值长度比的方向。
经线和纬线长度比:沿经线和纬线方向的长度比,用m和n表示。
任意一点与经线成α角方向上的长度比μαμα的计算公式:
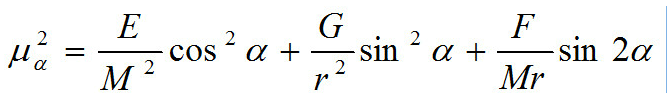
式中,M为子午圈曲率半径,r为纬圈半径,E,F,G称为一阶基本量(或高斯系数)
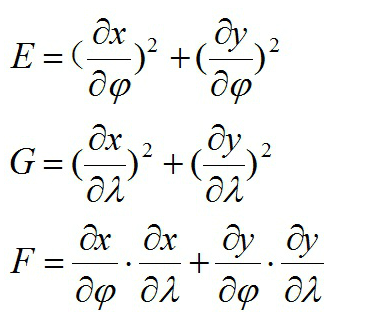
经线长度比:m=√EMm=EM纬线长度比:n=√Grn=Gr面积变形(area distortion)即面积比与1之差,Vp=p−1Vp=p−1所谓面积比是指:
地面上微分面积投影后的大小dF'与其相应的实地面积dF之比。
角度变形(angular distortion)
地面上某一角度投影前角值
ββ与其投影后的角值 β′β′之差,即β−β′β−β′。
投影中,一定点上的角度变形的大小用其最大值来衡量, 即称为该点最大角度变形ωω。sinω/2=(a−b)/(a+b)sinω/2=(a−b)/(a+b)tg(450+ω/4)= (a/b)1/2tg(450+ω/4)=(a/b)1/2其中a,b为该点的极值长度比。 补充知识:变形椭圆(indicatrix ellipse):

地面上的一个无穷小圆(微分圆)投影后一般成为一个微分椭圆,这个微分椭圆称为变形椭圆。
投影后为不同大小的圆形,则该投影为等角投影。
投影后为面积相等而形状不同的椭圆,则该投影为等面积投影。
投影后为面积不相等的椭圆,则该投影为任意投影。如果椭圆的某一半轴与微分圆的半径相等,如a=r,或b=r,则该投影为等距离投影。
下面是几种特殊投影的示例: